Binary Search on Array: Data Structures and Algorithms
Last modified - 28-04-2025
Author - Krishna Shinde
When it comes to efficient searching in an array, binary search is one of the most powerful algorithms in DSA (Data Structures and Algorithms). Whether you are preparing for interviews, programming contests, or simply looking to strengthen your DSA foundations, mastering binary search is a must.
In this article, we’ll explore what is binary search, how it works, why it’s better than linear search, and how it makes searching easy in DSA. We’ll also look at the real-world applications and a few important variations of binary search on arrays.
What is Binary Search?
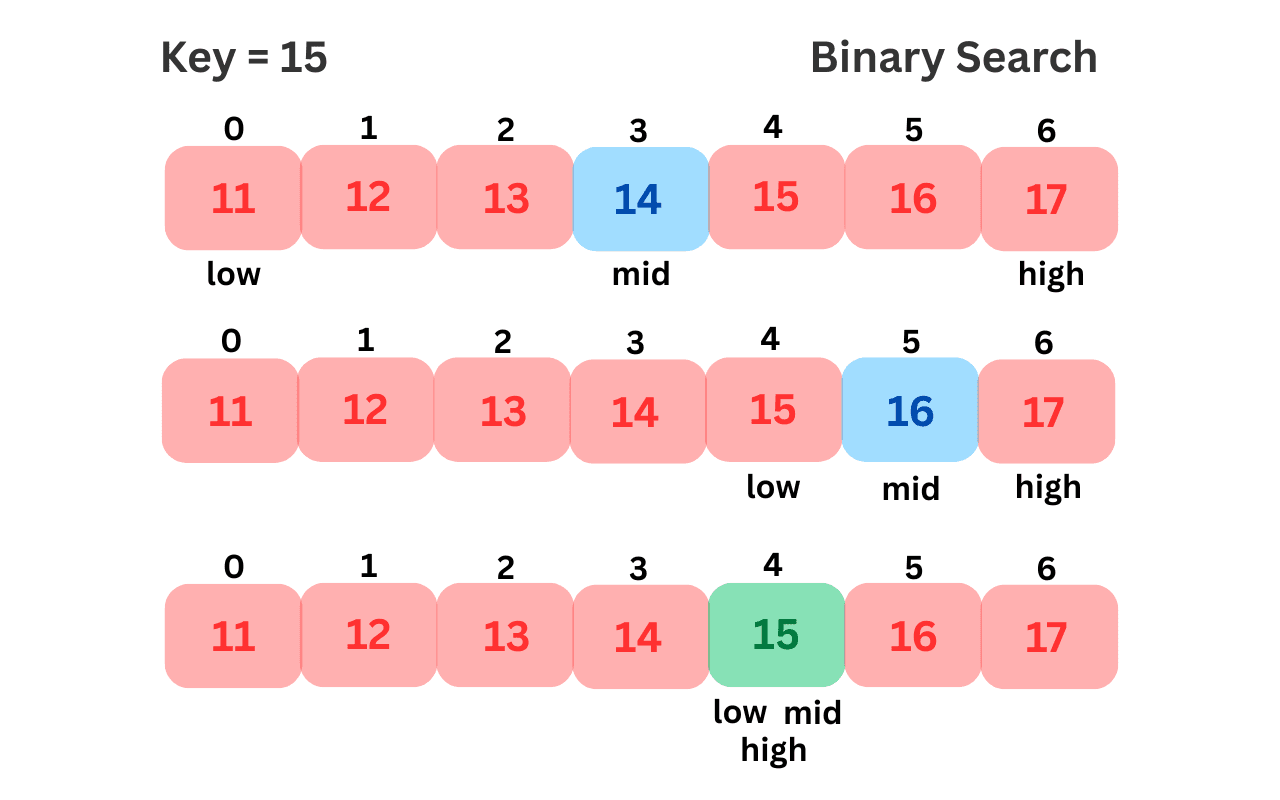
Binary search is an efficient algorithm for finding the index of an element in a sorted array. Unlike linear search, which traverses the entire array and checks each element, binary search divides the search space (array) into half during each iteration, drastically reducing the number of comparisons.
Important: Binary search only works on increasing and decreasing sorted arrays. If the array is unsorted, you must sort it first before applying binary search.
How Binary Search Works
Here’s a step-by-step explanation of how binary search works on an array:
This approach divides the problem in half during each step, making it extremely fast compared to linear search.
Time and Space Complexity of Binary Search
| Approach | Time Complexity | Space Complexity | Reason |
|---|---|---|---|
| Iterative Binary Search | O(log n) | O(1) | No extra memory used, constant space. |
| Recursive Binary Search | O(log n) | O(log n) | Due to recursive call stack depth. |
Binary Search Algorithm (Iterative Approach)
This is how you can implement binary search on an array using an iterative approach in C++:
#include <iostream> using namespace std; int binarySearch(int arr[], int n, int target) { int low = 0, high = n - 1; while (low <= high) { int mid = low + (high - low) / 2; // to prevent overflow if (arr[mid] == target) return mid; else if (arr[mid] < target) low = mid + 1; else high = mid - 1; } return -1; // element not found } int main() { int arr[] = {2, 4, 6, 8, 10, 12, 14}; int n = sizeof(arr) / sizeof(arr[0]); int target = 10; int result = binarySearch(arr, n, target); if (result != -1) cout << "Element found at index " << result; else cout << "Element not found"; return 0; }
Recursive Approach to Binary Search
Binary search can also be implemented using recursion.
int binarySearchRecursive(int arr[], int low, int high, int target) { if (low > high) return -1; int mid = low + (high - low) / 2; if (arr[mid] == target) return mid; else if (arr[mid] > target) return binarySearchRecursive(arr, low, mid - 1, target); else return binarySearchRecursive(arr, mid + 1, high, target); }
Applications of Binary Search
Binary search is not limited to finding a number in an array. It also has other uses, which include:
In DSA, binary search also forms the base for advanced techniques like binary search on functions, parametric search, and binary search over answers.
Common Binary Search Mistakes
While binary search is conceptually simple, it’s easy to make mistakes. Common mistakes include:
1. Infinite loops due to incorrect updating of start and end.
2. Errors when calculating midpoints.
3. Forgetting that binary search only works on sorted arrays.
4. Incorrectly handling duplicates if they exist in the array.
Practicing a variety of binary search problems can help you avoid these mistakes.
Conclusion
The binary search algorithm is one of the finest techniques that is used to search an element in an array by dividing the array in half during each iteration. In this article, we discussed binary search in detail. Follow Algoflame for more programming content.