Merge Sort Algorithm in Data Structure

Last modified - 31-05-2025

In data structures and algorithms, Merge sort is one of the concepts that every programmer must master. Merge sort stands out to be better than other sorting algorithms like Bubble sort, Insertion sort, and Selection sort. Merge sort is an efficient and powerful method, known for its divide-and-conquer strategy. It is widely used in various applications where large data sets need to be sorted.

In this DSA tutorial, we will explore Merge sort and how to implement Merge sort in C and C++. By the end, you will have a solid understanding of this important algorithm.

What is Merge Sort?

Merge sort is a comparison-based sorting algorithm that is based on the divide-and-conquer strategy. It breaks down a problem into smaller subproblems, solves them recursively, and then combines their solutions to solve the original problem.

The merge sort algorithm splits the array into two halves, sorts the left and the right parts individually using recursion, and then merges the left and the right parts into one.

How Does Merge Sort Algorithm Work

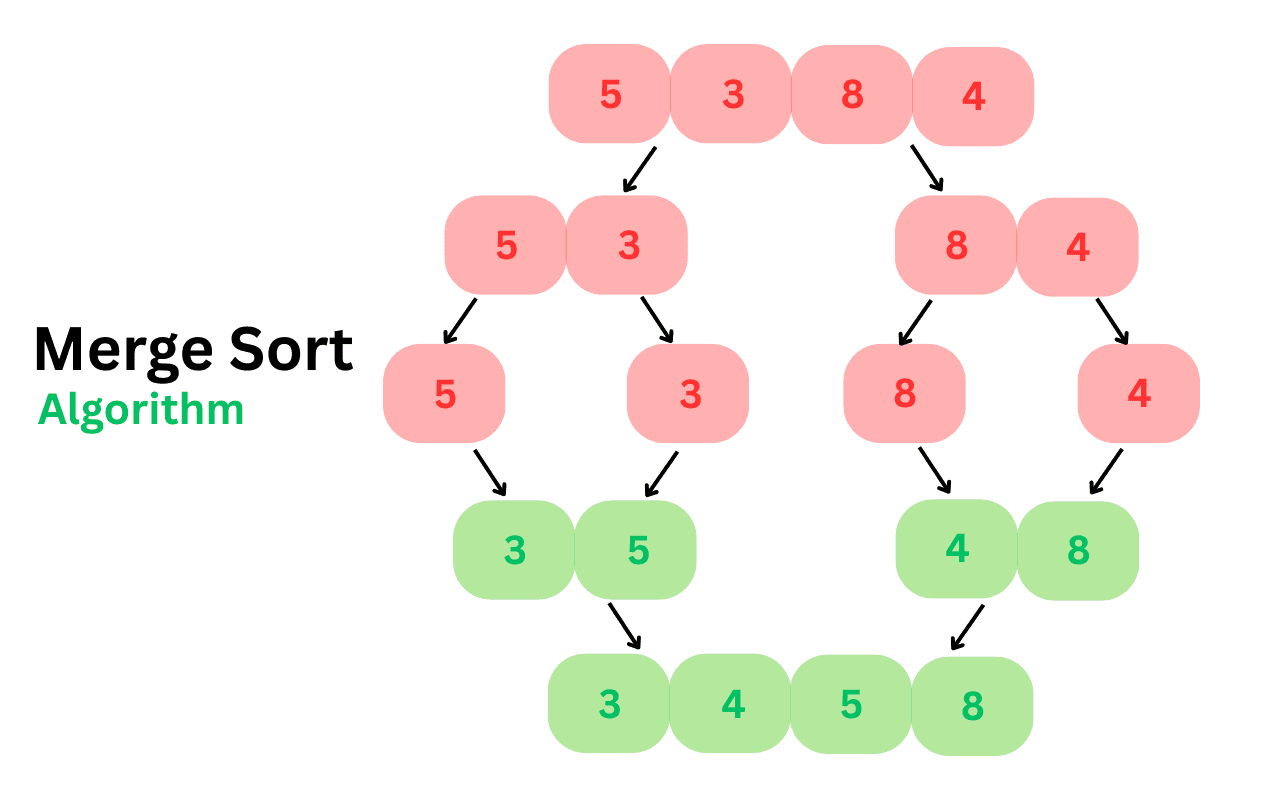
The algorithm for merge sort follows three major steps:

Divide: Split the array into two halves.
Conquer: Recursively sort the left and right half.
Combine: Merge the two sorted halves to produce the final sorted array.

Merge Sort C Program

#include <stdio.h>
#include <stdlib.h>

void merge(int arr[], int s, int mid, int e) {
    int nL = mid - s + 1;
    int nR = e - mid;

    // Create temporary arrays
    int* left = (int*)malloc(nL * sizeof(int));
    int* right = (int*)malloc(nR * sizeof(int));

    // Copy data to temp arrays
    for (int i = 0; i < nL; i++)
        left[i] = arr[s + i];
    for (int j = 0; j < nR; j++)
        right[j] = arr[mid + 1 + j];

    int i = 0, j = 0, k = s;

    // Merge the temp arrays back into arr[]
    while (i < nL && j < nR) {
        if (left[i] <= right[j]) {
            arr[k++] = left[i++];
        } else {
            arr[k++] = right[j++];
        }
    }

    // Copy remaining elements of left[], if any
    while (i < nL) {
        arr[k++] = left[i++];
    }

    // Copy remaining elements of right[], if any
    while (j < nR) {
        arr[k++] = right[j++];
    }

    // Free memory
    free(left);
    free(right);
}

void mergeSort(int arr[], int s, int e) {
    if (s >= e) return;

    int mid = s + (e - s) / 2;

    mergeSort(arr, s, mid);
    mergeSort(arr, mid + 1, e);
    merge(arr, s, mid, e);
}

int main() {
    int arr[] = {38, 27, 43, 3, 9, 82, 10};
    int n = sizeof(arr) / sizeof(arr[0]);

    printf("Original array: ");
    for (int i = 0; i < n; i++)
        printf("%d ", arr[i]);
    printf("
");

    mergeSort(arr, 0, n - 1);

    printf("Sorted array:   ");
    for (int i = 0; i < n; i++)
        printf("%d ", arr[i]);
    printf("
");

    return 0;
}

Merge Sort in C++

#include <iostream>
#include <vector>
using namespace std;

void merge(vector<int>& arr, int s, int e, int mid) {
    int nL = mid - s + 1;
    int nR = e - mid;

    // Temporary arrays
    int* left = new int[nL];
    int* right = new int[nR];

    // Copy data
    for (int i = 0; i < nL; i++)
        left[i] = arr[s + i];
    for (int j = 0; j < nR; j++)
        right[j] = arr[mid + 1 + j];

    int i = 0, j = 0, k = s;

    // Merge temp arrays
    while (i < nL && j < nR) {
        if (left[i] <= right[j])
            arr[k++] = left[i++];
        else
            arr[k++] = right[j++];
    }

    // Copy remaining elements
    while (i < nL)
        arr[k++] = left[i++];
    while (j < nR)
        arr[k++] = right[j++];

    delete[] left;
    delete[] right;
}

void mergeSort(vector<int>& arr, int s, int e) {
    if (s >= e) return;

    int mid = s + (e - s) / 2;
    mergeSort(arr, s, mid);
    mergeSort(arr, mid + 1, e);
    merge(arr, s, e, mid);
}

int main() {
    vector<int> arr = {38, 27, 43, 3, 9, 82, 10};
    mergeSort(arr, 0, arr.size() - 1);

    cout << "Sorted array: ";
    for (int num : arr)
        cout << num << " ";
    return 0;
}

Merge Sort Explanation Step by Step

Base case: If left >= right, the array has 0 or 1 element, so it’s already sorted. The function returns.

Divide:

int mid = left + (right - left) / 2; calculates the middle index.
mergeSort(arr, left, mid); recursively sorts the left half from left to mid.
mergeSort(arr, mid + 1, right); recursively sorts the right half from mid + 1 to right.

Conquer: Once both the halves are sorted, merge(arr, left, mid, right); and combine them into a single sorted subarray.

Time and Space Complexity of Merge Sort

Time Complexity: O(n log n)

Space Complexity: O(n) (due to temporary arrays used for merging)

When to Use Merge Sort

Use merge sort when:

You require stable sorting.
Working with linked lists (merge sort works well with linked lists due to O(1) space).
You’re sorting large datasets.

Merge Sort Comparison with Other Sorting Algorithms

Algorithm	Best Case	Average Case	Worst Case	Space Complexity	Stable
Merge Sort	O(n log n)	O(n log n)	O(n log n)	O(n)	Yes
Quick Sort	O(n log n)	O(n log n)	O(n²)	O(log n)	No
Bubble Sort	O(n)	O(n²)	O(n²)	O(1)	Yes
Insertion Sort	O(n)	O(n²)	O(n²)	O(1)	Yes

Conclusion

Merge Sort is an efficient, divide-and-conquer sorting algorithm that works well even for large datasets. Understanding how to implement and optimize merge sort will strengthen your knowledge of algorithms and recursion.

We’ve already written an article on bubble sort, so make sure to check that out too. Explore our coding tutorials to boost your programming skills. Follow Algoflame for more content on coding and data structures.